データが縦に3列以上並んでいる。L×Mのすべての組み合わせに対して、N回繰り返し測定したデータが入力されているパターンの統計処理方法

はじめに

分析手法は、
①何を見たいか、
②標本の数、
③データ型（比・間隔尺度・順序尺度・名義尺度）、
④データが正規分布に従うか（パラメトリックorノンパラメトリック）によって決まります。

今回は、②「標本の数」という観点から、どのような統計処理方法があるのか、ご紹介したいと思います。
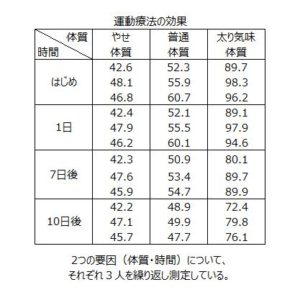
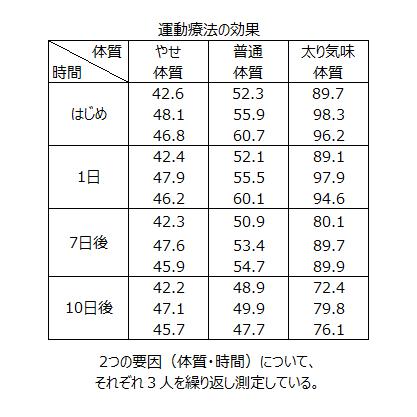
今回のデータのパターンは、『データが縦に3列以上並んでいて、L×Mのすべての組み合わせに対して、N回繰り返し測定したデータが入力されているパターン』をみていきます。
その他のパターンの統計処理方法についてはこちら

パターンの例

統計処理方法

上記のようなパターンに適切な統計処理方法は以下の方法があげられます。
1.グラフ表現
2.基礎統計量
3.2元配置分散分析と多重比較

グラフ表現

データの特徴を見るためには、グラフ表現が最も優れています。
ヒストグラム、度数分布表、棒グラフ、円グラフ、レーダーチャートなどのたくさんの種類があります。
今回のパターンのサンプルを利用すると、それぞれの3人の平均をとりグラフをかくと、変化が分かりやすく視覚化できるのではないでしょうか。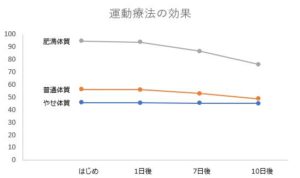

基礎統計量

・水準A（横）における平均と分散
・水準B（縦）における平均と分散
・２つの水準A,B（縦横）における平均と分散
・全体の平均
・それぞれの水準における母平均の区間推定など

2元配置分散分析と多重比較

横をみて・・・水準A₁、A₂、A₃、A₄の間に差があるのか。あるなら、どこに差があるのか。
縦を見て・・・水準B₁、B₂、B₃、B₄の間に差があるのか。あるなら、どこに差があるのか。
など、どの部分に差があるのかを知りたい場合は「2元配置分散分析」と「多重比較」をおこないます。
1元配置分散分析との大きな違いは、“２つの因子AとBの間の交互作用A×Bの存在”。　交互作用があるとわかれば、その先、慎重な判断が必要になってきます。