2つのグループA₁,A₂に対して、3つのカテゴリB₁,B₂,B₃の測定データが それぞれ入力されているパターン

はじめに

データを集めてみると、データのパターンが見えてきます。
そしてそれぞれのパターンによって、適切な統計処理方法が決まっています。

それぞれのパターンに沿って、どのような統計処理方法がとられるのかをご紹介したいと思います。
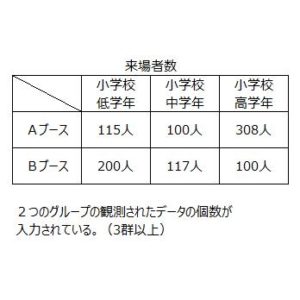
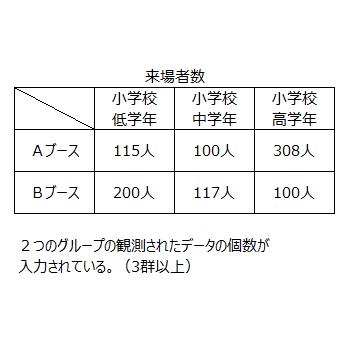
今回は、『表題と2つのグループA₁,A₂に対して、3つのカテゴリB₁,B₂,B₃の測定データが
それぞれ入力されているパターン』の統計処理方法についてご紹介します。
その他のパターンの統計処理方法についてはこちら

パターンの例

統計処理方法

上記のようなパターンに適切な統計処理方法は以下の方法があげられます。
1.グラフ表現
2.基礎統計量
3.同等性の検定
4.独立性の検定

グラフ表現

データの特徴を見るためには、グラフ表現が最も優れています。
ヒストグラム、度数分布表、棒グラフ、円グラフ、レーダーチャートなどのたくさんの種類があります。それぞれのグループのデータをグラフに表現して、可視化してみると色々なことが見えてきます。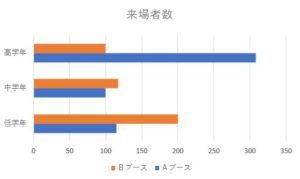

データの個数よりも、データが占める割合を表現するとわかりやすく可視化することができます。
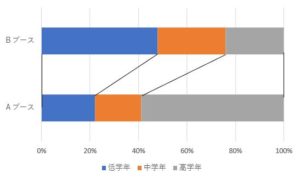
また、比率やパーセントで比較し、このようなグラフでもわかりやすく可視化ができます。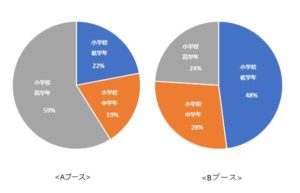

基礎統計量

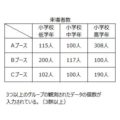
測定値ではなく、観測されたデータの個数なので、比率にすることがポイントです。
それぞれの標本比率を計算してみてください。

同等性の検定

グループAの中の3つの特性が起こる比率と、グループBの3つの特性が起こる比率が同じか、違いがあるのかを調べるには、同等性の検定を行います。

独立性の検定

グループA、グループBの間に、関連があるのかを調べるときは、独立性の検定を行います。