はじめに
データを集めてみると、データのパターンが見えてきます。
そしてそれぞれのパターンによって、適切な統計処理方法が決まっています。
それぞれのパターンに沿って、どのような統計処理方法がとられるのかをご紹介したいと思います。
今回は、『データが縦に3列以上並んでいて、表題と観測されたデータの個数が入力されているパターン』の統計処理方法についてご紹介します。
その他のパターンの統計処理方法についてはこちら
パターンの例
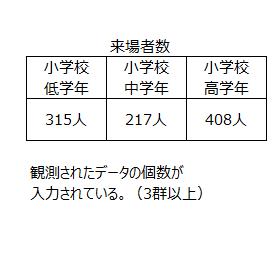
統計処理方法
上記のようなパターンに適切な統計処理方法は以下の方法があげられます。
1.グラフ表現
2.基礎統計量
3.適合度検定
グラフ表現
データの特徴を見るためには、グラフ表現が最も優れています。
ヒストグラム、度数分布表、棒グラフ、円グラフ、レーダーチャートなどのたくさんの種類があります。それぞれのグループのデータをグラフに表現して、可視化してみると色々なことが見えてきます。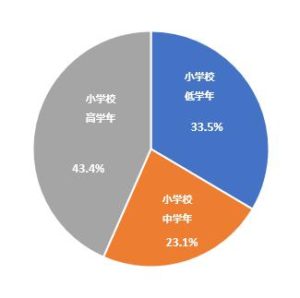
データの個数よりも、データが占める割合を表現するとわかりやすく可視化することができます。
基礎統計量
平均値や分散は算出することができません。
測定値ではなく、観測されたデータの個数なので、比率にすることがポイントです。
上記データ例とすると、
・「小学校低学年」の人の標本比率
= (315÷(315+217+408))×100 = 33.5106
・「小学校中学年」の人の標本比率
= (217÷(315+217+408))×100 = 23.0851
・「小学校高学年」の人の標本比率
= (408÷(315+217+408))×100 = 43.4043
適合度検定
理論値と実測値が一致しているかどうかを検定するために、適合度検定という検定を行います。
・曲線のあてはまりのよさ
・母集団の分布は正規分布に一致している?
・母集団の分布はポワソン分布と一致している?
・実験比率は理論比率と一致している?
などを見たい場合に使います。
検定の結果もしも、適合度の検定で適合していない(実測値と理論値は一致していない。当てはまりがよくない)というような結果が出た場合は、それ以降の分析は進めることができません。

コメント