データが縦に3列以上並んでいて、同じ変量を繰り返し測定したデータが入力されているパターンの統計処理方法

はじめに

データを集めてみると、データのパターンが見えてきます。
そしてそれぞれのパターンによって、適切な統計処理方法が決まっています。

それぞれのパターンに沿って、どのような統計処理方法がとられるのかをご紹介したいと思います。
今回は、『データが縦に3列以上並んでいて、同じ変量を繰り返し測定したデータが入力されているパターン』の統計処理方法についてご紹介します。
その他のパターンの統計処理方法についてはこちら

パターンの例

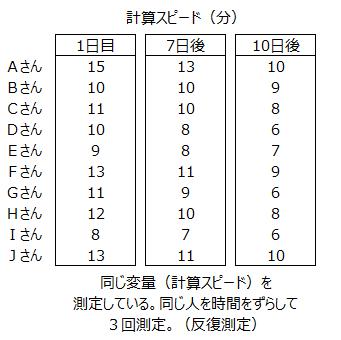
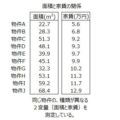
対応している3つのグループについて同じ変量を測定していることが特徴で、反復測定と呼ばれています。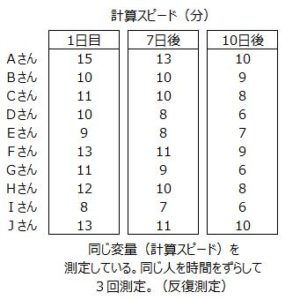

統計処理方法

上記のようなパターンに適切な統計処理方法は以下の方法があげられます。
1.グラフ表現
2.基礎統計量
3.反復測定による1元配置分散分析

グラフ表現

データの特徴を見るためには、グラフ表現が最も優れています。
ヒストグラム、度数分布表、棒グラフ、円グラフ、レーダーチャートなどのたくさんの種類があります。それぞれのグループのデータをグラフに表現して、可視化してみると色々なことが見えてきます。
反復測定を行った際のグラフ表現は、上記、パターンの例の、計算スピードの変化について測定したデータを例にしてグラフを書きますが、以下のようなグラフを書くと、変化をわかりやすく表現することができます。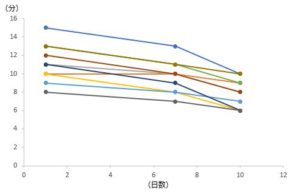

基礎統計量

グラフの特徴を数値でとらえるには、基礎統計量を算出する方法があります。
それぞれのグループの平均値、中央値、最頻値、最大値、最小値、分散、標準偏差、標本平均、標本分散、標本標準偏差などを算出し、グループの比較をしていきます。

反復測定による1元配置分散分析

「3つのグループ、変数1の母平均,変数2の母平均,変数3の母平均は同じである」と仮定して、グループ間に差がないことを検定をする際に、一元配置分散分析という手法を使います。
今回は、数値に反復測定をした値が入っているため、「反復測定による一元配置分散分析」といった手法を使います。
検定の結果仮説が棄却され、「3つのグループ間に差がある」という結果になり、どこに差があるのかを見ていく際の手法として、『多重比較』という手法を使います。