はじめに
データを集めてみると、データのパターンが見えてきます。
そしてそれぞれのパターンによって、適切な統計処理方法が決まっています。
それぞれのパターンに沿って、どのような統計処理方法がとられるのかをご紹介したいと思います。
今回は、『データが縦に3列以上並んでいて、それらの3列の変量は種類の異なるデータが入力されているパターン』の統計処理方法についてご紹介します。
その他のパターンの統計処理方法についてはこちら
パターンの例
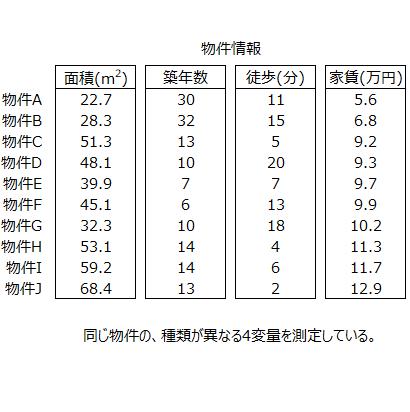
1つの事柄に対して、種類の異なる3変量以上のデータが入っているので、変量間の関係や、変量の総合化、変量の共通点などを調べてみたくなりますよね。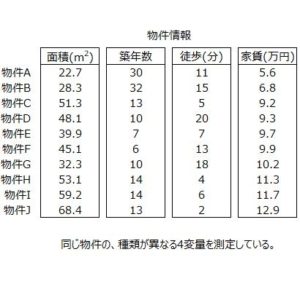
統計処理方法
上記のようなパターンに適切な統計処理方法は以下の方法があげられます。
1.グラフ表現
2.基礎統計量
3.重回帰分析
4.主成分分析
5.因子分析
グラフ表現
今回のパターンの場合は、同じものに関する3つの値を測定しているため、平面上にグラフを書くことができません。立体的な散布図を書くか、2つの変量に制限して散布図を書いてみるという表現方法があります。
基礎統計量
変量間の関係性を表現してくれる統計量がとても重要になってきます。
相関行列や分散共分散行列を使って表現してみましょう。
| X1 | X2 | X3 | |
| X1 | 1 | 相関係数 | 相関係数 |
| X2 | 相関係数 | 1 | 相関係数 |
| X3 | 相関係数 | 相関係数 | 1 |
↑相関行列
↓分散共分散行列
| x1 | x2 | x3 | |
| x1 | 分散 | 共分散 | 共分散 |
| x2 | 共分散 | 分散 | 共分散 |
| x3 | 共分散 | 共分散 | 分散 |
重回帰分析
3つ以上の変量間に原因と結果の関係がある場合、重回帰分析をしてみると、結果を予測したり、原因を特定したりすることができます。
今回のサンプルデータの場合、面積、築年数、徒歩が「原因」、家賃を「結果」と考えてみると、別のあらたな「物件K」が出てきたときに、面積、築年数、徒歩時間から、家賃を予測することができたりします。
また、どの変量が結果に大きな影響を与えている因子なのかという判定をすることもできます。
主成分分析
3つ以上のデータを1つにまとめたいときは、主成分分析を行います。
主成分分析を行うと、総合的評価や順位付けをすることができます。
因子分析
因子分析は、3つ以上の変量間に共通する原因を調べたいときに因子分析を行います。

コメント